Statistika: Standardna devijacija

Standardna devijacija predstavlja mjeru raspršenosti podataka u nekom skupu (mjerenju). Oznaka za standardnu devijaciju je $\sigma$, a računa se kao kvadratni korijen iz varijanse.

Varijansa (disperzija) se definiše kao odstupanja slučajne varijable od njene srednje vrijednosti. Izračunava se na sljedeći način:

• izračuna se srednja vrijednost varijable $\bar{x}$,
• za svaku vrijednost nađe njena razlika od srednje vrijednosti i kvadrira$(x_i-\bar{x})^2$,
• zatim se nađe srednja vrijednost svih kvadrata razlika iz drugog koraka.

$$ Var = \frac{1}{N}\sum_{i=1}^{N}(x_i-\bar{x})^2$$

Primjer

Pretpostavimo da smo upravo izmjerili visine (u milimetrima) za pet pasa (slika):

Izmjerene visine (u nivou ramena) su redom: 600 mm, 470 mm, 170 mm, 430 mm i 300 mm. Odredimo srednju vrijednost, varijancu i standardnu devijaciju.

Srednja vrijednost:

$$ ar{x}= \frac{600 + 470 +170 + 430+ 300 }{5}=394\, mm$$

Dakle, srednja (prosječna) visina je 394 mm. Na slici to izgleda ovako:

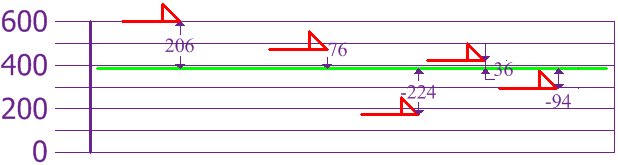
Izračunajmo sada razliku visine za svakog psa u odnosu na srednju vrijednost. Kako se vidi na slici ispod one iznose 206 mm, 76 mm, -224 mm, 36 mm i -94 mm.

Varijansa se dobije kada se svaku od ovih razlika kvadriramo i izračunamo srednju vrijednost dobijenih kvadrata:

$$ Var = \sigma ^2=\frac{206^2+76^2+(-224)^2+36^2+(-94)^2}{5}=21704\, mm^2$$

Na kraju, standardna devijacija se dobije kao kvadratni korijen varijanse:

$$\sigma = \sqrt{\sigma^2}=147\, mm$$

Kada znamo vrijednost standardne devijacije, onda možemo odrediti da li neka vrijednost leži unutar ili izvan "normalnih" vrijednosti, tj. da li ima preveliku ili premalu vrijednost. U primjeru sa psima, vidimo da visine za tri psa leže u normalnim vrijednostima (unutar jedne standardne devijacije u odnosu na srednju vrijednost), a dvije visine su izvan tog opsega (prvi pas - rotvajler je visok pas, a treći - jazavičar je nizak pas).

Možemo očekivati da 68% od svih promjenljivih leži unutar jedne standardne devijacije (standardna normalna raspodjela).

U ovom primjeru je korištena populacija od 5 pasa (tj. oni su bili jedini za koje smo bili zainteresovani). Međutim, češće se susrećemo sa problemima u kojima nemamo podatke za cijelu populaciju (visine svih pasa u nekom gradu ili regiji), i u tom slučaju naši podaci predstavljaju uzorak (dio populacije). Tada se formule za izračunavanje varijanse razlikuju (dijelimo sa $N-1$ umjesto sa $N$).

Konkretno, ako govorimo o ovih pet pasa kao dio veće populacije, tada imamo uzorak, pa će varijansa i srandardna devijacija biti jednake:

$$  Var = \sigma ^2=\frac{206^2+76^2+(-224)^2+36^2+(-94)^2}{4}=27130\, mm^2$$

$$\sigma = \sqrt{\sigma^2}=164\, mm$$

Sažetak:

Standardna devijacija za populaciju: $ \sigma=\sqrt{\frac{1}{N}\sum_{i=1}^{N}(x_i - \mu)^2}$

Standardna devijacija za uzorak: $ s=\sqrt{\frac{1}{N-1}\sum_{i=1}^{N}(x_i - \bar{x})^2}$

Oznake $\sigma$ i $s$, odnosno $\mu$ i $\bar{x}$ imaju ista značenje, a služe samo da naglase kada govorimo o populaciji, a kada o uzorku.

Reference: mathisfun.com, wikipedia